Интересный предел от Владимира Арнольда
from pstt
Предисловие
В данный момент читаю книгу “Наглядная дифференциальная геометрия и формы” Тристана Нидэма. Ее особенностью является то, что вместо классического понимания предела используется геометрический подход Ньютона. В одном из первых заданий, для тренировки этого геометрического подхода, Тристан дает интересный предел, который в свою очередь предложил Владимир Арнольд в своей книге “Гюйгенс и Барроу, Ньютон и Гук: первые шаги математического анализа и теории катастроф, от эвольвент до квазикристаллов”.
Вот этот предел:
$$ \lim_{x \to 0} \frac{\sin\tan{x} – \tan\sin{x}}{\sin^{-1}\tan^{-1}{x} – \tan^{-1}\sin^{-1}{x}} $$
Оказывается Арнольд (по крайней мере по словам Тристана) также был сторонником геометрического подхода, поскольку он дает больше понимания, чем “сухое” чисто алгебраическое определение предела.
Так вот, взять этот предел у меня не получилось. Ни с подходом Ньютона, ни как иначе. Кстати говоря, Арнольд сказал, что единственный математик, который смог быстро взять этот предел, был лауреат Филдсовской премии Герд Фальтингс.
Оставив свои попытки, я полез в интернет и нашел статью, в которой этот предел был решен и классически, и по Ньютону. Поэтому здесь ниже я хочу привести перевод этой статьи на великий и могучий. Также хочу выразить благодарность автору Mihai Maruseac оригинальной статьи за его работу.
Об этом пределе из VDGF
Прим. переводчика: VDGF = Visual Differential Geometry and Forms: A Mathematical Drama in Five Acts by Tristan Needham
В конце последнего раздела предыдущей статьи я показал предел, который был дан в качестве упражнения в “Наглядная дифференциальная геометрия и форма: Математическая драма в пяти частях” Тристана Нидэма. В последней статье я подготовил все необходимое, чтобы взять этот предел в этой статье. Так что, давайте сделаем это.
Напомню, нам нужно вычислить следующий предел:
$$ \lim_{x \to 0} \frac{\sin\tan{x} – \tan\sin{x}}{\sin^{-1}\tan^{-1}{x} – \tan^{-1}\sin^{-1}{x}} $$
Я возьму этот предел несколькими способами, что может показаться несколько сложным. Но есть и простое решение данной задачи. И если вы не хотите читать статью полностью, можете сразу перейти к разделу с простым решением.
Анализ и алгебра
Мы знаем, что $\sin{0} = 0$ и $\tan{0}= 0$, поэтому очевидно, что наш предел это случай неопределенности $\frac{0}{0}$. Наивно было бы использовать правила Лопиталя. А также быстрая попытка посчитать первые производные для слагаемых в числителе дает понять, что использование правила Лопиталя было бы Сизифовым трудом:
$$ \frac{d\sin{\tan{x}}}{dx} = \frac{\cos{\tan{x}}}{\cos^2{x}} $$ $$ \frac{d\tan{\sin{x}}}{dx} = \frac{\cos{x}}{\cos^2{\sin{x}}} $$
В свою очередь, используя приближения $\sin{x}\asymp x$ и $\tan{x} \asymp {x}$, мы заметим, что первая производная до сих пор сводит числитель к $0$, а значит нам нужно посчитать и вторые производные! Или даже больше – как мы увидим позже.
Обращаться к ChatGPT или Bard бесполезно. Поскольку работая с приведенными выше сложными выражениями (или подобными), оба эти ИИ начинают отбрасывать тригонометрические функции, преобразовывая, например $\cos{\sin{x}}$ в $\cos{x}$ и тем самым получая неправильные ответы. WolframAlpha дает результат для предела равный 1, но очевидно, что это читерство, и мы ничему не научимся, поступив таким образом.
Следующий подход это попытаться раскладывать в ряды Тейлора в окрестности $0$ до тех пор, пока мы не получим различные слагаемые (гарантированно, поскольку $\sin\tan{x} \neq \tan\sin{x}$ в общем случае). Однако вычисление этих рядов Тейлора непосредственно приводит к вычислению тех же производных, что и раньше, поэтому все еще требуется большой объем работы.
Упрощай и побеждай с помощью алгебры
Вместо этого, давайте посмотрим на вид предела. Пусть $f(x) = \sin\tan{x}$ и $g(x) = \tan\sin{x}$, тогда предел примет вид:
$$ \lim_{x\to 0} \frac{f(x)-g(x)}{g^{-1}(x)-f^{-1}(x)} $$
Отсюда видно, что мы можем уменьшить необходимую работу, если сможем найти взаимосвязь между рядами Тейлора для $f^{-1}$ (или $g^{-1}$) и $f$ (или $g$). Мы можем вычислить коэффициенты исходной функции (используя огромное количество труда, считая все эти производные упомянутые выше) и затем следовать алгоритму для определения коэффициентов обратной функции.
К счастью, такой алгоритм существует, при определенных условиях, поскольку есть взаимосвязь между функцией и ее обратной: их композиция должна давать тождественную функцию. То есть:
$$ f(f^{-1}(x)) = x $$
Предположим, что у нас есть прекрасная функция $f$ такая, что мы можем записать для $f$ и ее обратной разложение в ряд Тейлора в окрестности нуля, используя некоторые коэффициенты:
$$ f(x) = a_0 + a_1 x + a_2 x^2 + \dots = \sum_{i=0}^{\infty} a_i x^{i} $$
$$ f^{-1}(x) = A_0 + A_1 x + A_2 x^2 + \dots = \sum_{i=0}^{\infty} A_i x^{i} $$
Нас волнует только то, сходятся ли эти ряды вокруг $0$, поскольку именно там мы хотим вычислить предел. Это также означает, что мы можем сократить ряд до конечного числа коэффициентов. Если мы можем вычислить каждый $A_i$ из этого конечного множества, используя только конечное множество $a_i$, то мы получили наш алгоритм.
Начнем с того, что мы предполагаем очень узкий интервал, где мы можем аппроксимировать каждую функцию линейными членами (предполагая, что $a_1 \neq 0$ и $A_1 \neq 0$). Таким образом,
$$ f(x) = a_0 + a_1 x $$
$$ f^{-1}(x) = A_0 + A_1 x $$
В данном случае, имеем следующее:
$$ \begin{align} f(f^{-1}(x)) &\asymp a_0 + a_1 f^{-1}(x) \asymp\\ &\asymp a_0 + a_1(A_0+A_1 x) = (a_0 + a_1 A_0) + a_1 A_1 x \end{align} $$
Поскольку данное выражение должно равняться $x$, имеем
$$ \begin{cases} a_0 + a_1 A_0 = 0\\ a_1A_1 = 1 \end{cases} $$
Отсюда,
$$ \begin{aligned} A_0 &= \frac{-a_0}{a_1}\\ A_1 &= \frac{1}{a_1} \end{aligned} $$
Это было тривиально, давайте рассмотрим до второго порядка:
$$ \begin{align} f(x) &= a_0 + a_1x + a_2x^2\\ f^{-1}(x) &= A_0 + A_1x + A_2x^2 \end{align} $$
Отсюда имеем:
$$ \begin{align} f(f^{-1}(x)) &\asymp a_0 + a_1f^{-1}(x) + a_2\left(f^{-1}(x)\right)^2\\ &\asymp a_0 + a_1\left(A_0 + A_1x + A_2x^2\right) + a_2\left(A_0 + A_1x + A_2x^2\right)^2 \end{align} $$
Стало немного сложнее, но нас интересуют только коэффициенты при членах со степенями не больше 2. Поэтому, после раскрытия скобок мы игнорируем все что выше данной степени. Требуя, чтобы коэффициенты были при одинаковых множителях, получим:
$$ \begin{cases} a_0 + a_1A_0+a_2A_0^2 = 0\\ a_1A_1 + 2a_2A_0A_1 = 1\\ a_1A_2 + a_2A_1^2 = 0 \end{cases} $$
Из первого уравнения мы можем определить $A_0$, используя квадратичную формулу. Замена во втором дает $A_1$, а затем мы получаем $A_2$ из последнего уравнения. Это не намного сложнее, чем когда мы остановились на первом члене, у нас есть только одно квадратичное уравнение, а все остальные линейны.
Но сможем ли мы продолжить процесс, чтобы определить все необходимые коэффициенты $A_i$? Если нет, то нужно возвращаться к доске и искать другой подход. К счастью, он работает: в разложении в ряд Тейлора функции $f(f^{-1}(x))$ каждый $A_i$ сначала встречается при множителе $x^{i}$. Таким образом, если мы хотим вычислить $n$ коэффициентов разложения в ряд Тейлора обратной функции, то нам нужно вычислить только $n$ коэффициентов исходной функции, раскладываем $f(f^{-1}(x))$ и затем решаем систему из $n$ уравнений, которая получается при сопоставлении коэффициентов при одинаковых множителях $x^{i}$. Для $A_0$ получаем уравнение степени $n$, так как мы получаем по члену от каждого множителя $x^{i}$. При этом остальные неизвестные будут найдены, решая линейное уравнение. Запомните этот момент, поскольку мы вернемся к нему позже.
Продолжая таким образом, если мы не хотим строить систему из $n$ уравнений, мы можем воспользоваться теоремой, дающую коэффициенты напрямую, но здесь все равно не меньше работы.
Всё это приводит нас к вопросу: как много коэффициентов нам надо, чтобы вычислить предел?
Упрощение на основе симметрии
Вместо того, чтобы ответить на вопрос, давайте посмотрим можем ли мы еще что-то “выудить” из формулировки задачи, чтобы уменьшить нашу работу. Пусть опять $f$ и $g$:
$$ f(x) = \sin\tan{x} $$ $$ g(x) = \tan\sin{x} $$
Что если мы упростим еще больше? Пусть $u(x) = \sin{x}$ и $v(x) = \tan{x}$. Тогда $f = u \circ v$ и $g=v \circ u$, просто композиция функций, при этом $u$ и $v$ располагаются симметрично. Отсюда, наш предел примет вид:
$$ \lim_{x\to 0} \frac{(u\circ v)(x) – (v\circ u)*(x)}{(u^{-1} \circ v^{-1})(x) – (v^{-1} \circ u^{-1})(x)} $$
Хоть этот вид и выглядит несколько сложнее, но он нам поможет определить как много членов разложения в ряд Тейлора нам нужно вычислить. Мы можем начать с разложения для $\sin{x}$ и $\tan{x}$, получить разложение для $f$ и $g$ и для их разности. Далее мы возьмем первый коэффициент не равный нулю и используя алгоритм из предыдущего раздела определим коэффициенты ряда Тейлора для знаменателя. Звучит как план, но подождите, мы можем сделать еще меньше работы!
Обе функции $\sin{x}$ и $\tan{x}$ имеют еще одну симметрию, которой мы можем воспользоваться: они обе нечетные функции. Это означает, что их разложение в ряд Тейлора содержит только члены $x^k$, где $k$ – нечетные числа. Это также означает, что их композиция — тоже нечетная функция, то есть аналогично имеет в разложении члены только с нечетной степенью. Можем ли мы определить эти коэффициенты по коэффициентам функции Тейлора? Прим. переводчика: тут я не очень понял....
Предположим, что
$$ \begin{align} u(x) &= d_1 x + d_3 x^3 + d_5 x^5 + d_7x^7+\dots\\ v(x) &= c_1 x + c_3 x^3 + c_5 x^5 + c_7x^7+\dots \end{align} $$
Если мы остановимся на линейном члене, то имеем:
$$ u(v(x)) \asymp d_1c_1x $$
Это симметричный член, поэтому он будет такой же как и у $v(u(x))$. Потому разность будет равна 0, то есть мы до сих пор имеет предельный случай $\frac00$.
Если попробуем разложить до кубического члена, то имеем;
$$ u(v(x)) \asymp d_1c_1x + (d_1c_3 + d_3c_1)x^3 $$
Все еще симметрично, попробуем разложить до 5 степени:
$$ \begin{align} u(v(x)) &\asymp d_1c_1x + (d_1c_3 + d_3c_1)x^3 +\\ &+ (d_1c_5 + 3d_3c_1^2c_3 + d_5c_1)x^5 \end{align} $$
Больше не симметрично, так как если поменять все $d$-шки на $c$-шки получится другое выражение. Поэтому в данном случае $u(v(x)) – v(u(x))$ даст ненулевое значение при множителе $x^5$. Но поможет ли это нам?
Оказывается, что наш предел требует еще одного дополнительного шага. Так как:
$$ \begin{align} \sin{x} \asymp x – \frac{x^3}{6} + \frac{x^5}{120} \tan{x} \asymp x + \frac{x^3}{3} + \frac{2x^5}{15} \end{align} $$
То есть, $d_1=c_1=1$ и наше получившееся выражение оказывается все еще симметричным. Потому давайте разложим до 7 степени. Теперь:
$$ \begin{align} u(v(x)) &\asymp x + (c_3 + d_3) x^3 + (c_5+3d_3c_3+d_5)x^5 +\\&+ (c_7+3d_3c_5 + 3d_3c_3^2 + 5d_5c_3 + d_7)x^7 \end{align} $$
Теперь коэффициент при $x^7$ не симметричный. Теперь вычислим разницу:
$$ u(v(x)) – v(u(x)) \asymp (2(d_5c_3-d_3c_5) + 3d_3c_3(c_3-d_3)))x^7 $$
Если мы заменим в выражении $u=\sin{x}$ и $v = \tan{x}$, то получим:
$$ \sin\tan{x} – \tan\sin{x} \asymp -\frac{x^7}{30} $$
Что это значит? Мы знаем, что нам нужно вычислять вплоть до 7 производной для всех задействованных членов (хотя нам нужна только половина из них из-за нечетности функций). Мы также знаем, что $\sin\tan{x} \leq \tan\sin{x}$ на небольшом интервале $(0, \alpha)$ до того как член $x^9$ становится значимым.
Теперь, наконец, мы можем вычислить предел.
Вычисление предела алгебраически
Теперь, когда наш перебор дал понять сколько производных нам нужно считать, мы можем вернуться к нашему алгоритму, данному 2 раздела назад. Мы знаем, что нам надо выразить $f$ и $g$ вплоть до 7-го порядка разложения в ряд Тейлора и затем вычислить коэффициенты $A_i$ для соответствующих обратных функций. То есть для каждой функции там надо 8 коэффициентов, а всего выходит 28 значений для расчета?
Так, подождите. Мы знаем, что все функции нечетные и это уменьшает вдове число членов в разложении. Мы также знаем, что первые производные для $f$ и $g$ равны $1$. Потому нам нужно вычислить только $a_3,~a_5,~a_7$ с помощью производных и $A_3,~A_5,~A_7$ с помощью описанного выше алгоритма (дважды, один раз для $f$, один раз для $g$). Всего лишь 12 значений. Начнем?
Ну, давайте подумаем еще немного, мы увидели, что все коэффициенты в $f-g$ вплоть до 7 порядка сокращаются. Справедливо ли это для коэффициентов в $g^{-1} – f^{-1}$?
Если вы помните алгоритм для вычисления $A_i$, только $A_0$ участвовал в нелинейном уравнении. К счастью для нас, $A_0 = 0$ (для $f$ и для $g$), поэтому у нас есть только линейные уравнения. Но это также означает, что мы можем записать каждый $A_i$ как линейную комбинацию $a_1, a_2, \dots, a_i$ (где $A_1, A_2, \dots, A_{i-1}$ могут появляться как коэффициенты линейного выражения).
Но мы также знаем, что для нашего предела $a_1=A_1=1$. Это означает – упражнение оставлено читателю, вы можете доказать это по индукции – что каждый $A_i$ может быть записан как $A_i = -a_i + P_i(a_2, a_3, \dots, a_{i-1})$, где $P_i$ – линейная комбинация, которая получается решением соответствующей системы уравнений.
В частности, если $f$ и $g$ имеют общие несколько коэффициентов (как мы уже видели $a_1=b_1=1,~a_3=b_3$ и $a_5 и b_5$ и все оставшиеся до 8 степени равны 0), поэтому их обратные также имеют общие коэффициенты. Отсюда, единственные коэффициенты имеющие значение – $a_7,~b_7,~A_7$ и $B_7$. Предел тогда сводится к:
$$ \frac{a_7 – b_7}{B_7 – A_7} = \frac{a_7 – b_7}{a_7-b_7} = 1 $$
Это потому, что один и тот же полином $P_7$ встречается и в $B_7 = -b_7 + P_7$ и в $A_7 = a_7 + P_7$ и все коэффициенты равны.
Итак, в итоге мы вычислили предел без необходимости вычислять какие-либо производные, а только с учетом соответствующих соотношений симметрии. Нам все еще нужно было проделать большую алгебраическую работу, чтобы доказать некоторые вспомогательные леммы (которые полезны в других подобных случаях). Нет ли более быстрого подхода?
Геометрическое решение
Предел был дан, как пример того, что геометрический подход может быть быстрее чем алгебраические манипуляция. Итак, нам нужно вычислить предел с помощью геометрии. Мы знаем, что наши функции $f(x) = \sin\tan{x}$ и $g(x) = \tan\sin{x}$ равны 0 в 0 и имеют производную равную 1. Давайте построим графики $f,~g$ и их обратных в области их линейности (и увеличим углы наклона):
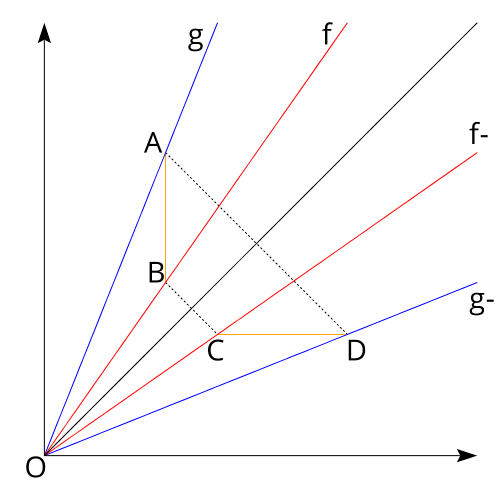
Этот график получается таким, потому что $f \leq g$ (доказано два раздела назад) и $x\leq f(x)$ (легко доказать). Черная диагональ обозначает линию $y=x$, голубые линии – $g$ и $g^{-1}$, красные – $f$ и $f^{-1}$. Из определения обратной функции график симметричен относительно диагональной линии.
Нам просто нужно вычислить отношение $AB$ к $CD$ по мере того как они становятся ближе к началу отсчета. Из-за симметрии эти два отрезка оказываются равными. Отсюда следует, что предел равен 1.
Аналогично доказывается для случая, если $f$ и $g$ были бы по разные стороны диагонали $y=x$.
Заключение
Мы доказали, что если у нас есть две нечетные функции $u$ и $v$ такие, что их производные в 0 равны 1 и $u \circ v \neq v\circ u$, тогда предел
$$ \lim_{x\to 0} \frac{(u\circ v)(x) – (v\circ u)*(x)}{(u^{-1} \circ v^{-1})(x) – (v^{-1} \circ u^{-1})(x)} $$
существует и равен 1. Это было доказано быстро с помощью геометрического подхода, но также решено и с помощью алгебраических операций. Эти алгебраические операции также позволяет вычислить предел, приведенный выше, когда производные $u$ и $v$ в 0 не равны 1, мы просто должны решить определенную систему линейных уравнений, полагая, что предел существует. Если функции не нечетные, нам также нужно было бы решить нелинейное уравнение, делая задачу сложнее.
Источники:
- Tristan Needham, Visual Differential Geometry and Forms: A Mathematical Drama in Five Acts – Princeton University Press, 2021 https://doi.org/10.2307/j.ctv1cmsmx5
- Оригинальная статья: Mihai Maruseac. About that limit from VDGF – 2022 – https://mihai.page/about-that-limit/#symmetry-based-simplification
